Die Wellenfunktion eines Teilchens hat tatsächlich keine physikalische Interpretation, bis ein Operator wie der Hamilton-Operator darauf angewendet wird oder wenn Sie es quadrieren, was seine Wahrscheinlichkeit angibt, an einem bestimmten Ort zu sein. Eine negative Wellenfunktion bedeutet also physikalisch nichts. Nehmen wir jedoch für ein Teilchen in einer Box an, wenn Sie den Impulsoperator für den stationären Zustand $ n ^ \ text {th} $ lösen, erhalten Sie zwei Lösungen: $ + \ hbar k $ und $ - \ hbar k $ , wobei $ k = n \ pi / L $. Die Plus- und Minuszeichen bedeuten, dass eine Wahrscheinlichkeit von 50 $% besteht, dass sich das Partikel von links nach rechts bewegt, und eine Wahrscheinlichkeit von 50 $%, dass sich das Partikel von rechts nach links bewegt.

Wenn zwei Wellenfunktionen summiert werden, um die Wellenfunktion eines Molekülorbitals zu erhalten, bedeutet eine negative Wellenfunktion überhaupt nichts. Der Grund, warum beim Hinzufügen einer positiven und negativen Wellenfunktion ein antibindendes Orbital gebildet wird, liegt einfach darin, dass Sie beim Hinzufügen einer positiven und negativen Zahl $ 0 $ oder eine wirklich kleine Zahl erhalten. Dies ist als destruktive Interferenz bekannt. Daher enthält die neue Wellenfunktion einen Bereich, in dem die y-Werte gleich $ 0 $ sind. Wenn Sie also diese neue Wellenfunktion des Molekülorbitals quadrieren, werden Sie feststellen, dass die Wahrscheinlichkeit sehr hoch ist, das Elektron in dieser Position zu finden (bekannt als Knotenebene), und daher wird es als antibindendes Orbital bezeichnet. Beachten Sie jedoch, dass gerade Da sich in der Wellenfunktion ein negativer Bereich befindet, bedeutet dies nicht, dass sich immer ein Anti-Bonding-MO bildet. Wenn Sie beispielsweise 2 negative Wellenfunktionswerte hinzufügen (als konstruktive Interferenz bezeichnet), erhalten Sie einen großen negativen Wert. Wenn Sie quadrieren, wird ein sehr großer positiver Wert. Dies bedeutet also, dass eine große Wahrscheinlichkeit besteht, dass sich das Elektron in dieser Region befindet, und dass es sich daher um ein bindendes MO handelt.

Zusätzlich zu @ Nanoputians hervorragender Beschreibung konstruktiver und destruktiver Interferenzen bei der Bildung von MOs möchte ich eine mathematischere Erklärung dafür liefern, warum die Phase der Wellenfunktion keine Rolle spielt.

Finden der Wellenfunktion

Die zeitunabhängige Schrödinger-Gleichung lautet in einer Dimension:

$$ \ hat {H} \ psi (x) = E \ psi (x) $ $

Es kann gezeigt werden, dass, wenn eine Wellenfunktion $ \ psi = \ psi (x) $ die obige Gleichung erfüllt, die Wellenfunktion $ k \ psi $ (mit $ k \ in \ mathbb {C}) erfüllt. $) erfüllt auch die obige Gleichung mit dem gleichen Energieeigenwert $ E $. Dies liegt an der Linearität des Hamilton-Operators:

$$ \ begin {align} \ hat {H} (k \ psi) & = k (\ hat {H}) \ psi) \\ & = k (E \ psi) \\ & = E (k \ psi) \ end {align} $$

Es gibt mehrere Bedingungen, die eine Wellenfunktion erfüllen muss es muss physikalisch realisierbar sein, dh es soll ein "reales" physikalisches Teilchen darstellen. In dieser Diskussion ist die relevante Bedingung, dass die Wellenfunktion quadratintegrierbar (oder normalisierbar ) sein muss. In mathematischen Begriffen:

$$ \ langle \ psi \ lvert \ psi \ rangle = \ int _ {- \ infty} ^ {\ infty} \! \ Lvert \ psi \ rvert ^ 2 \, \ mathrm {d} x < \ infty $$

Dies bedeutet, dass in \ mathbb {C} $ eine Konstante $ N \ existieren muss, sodass $ N \ psi $ normalisiert em ist >:

$$ \ int _ {- \ infty} ^ {\ infty} \! \ lvert N \ psi \ rvert ^ 2 \, \ mathrm {d} x = \ lvert N \ rvert ^ 2 \! \! \ int _ {- \ infty} ^ {\ infty} \! \ lvert \ psi \ rvert ^ 2 \, \ mathrm {d} x = 1 $$

Von diesem Punkt an Wir gehen davon aus, dass wir bereits die geeignete Normalisierungskonstante gefunden haben, so dass die Wellenfunktion $ \ psi $ bereits normalisiert ist. Mit anderen Worten, nehmen wir an, $ \ langle \ psi \ lvert \ psi \ rangle = 1 $, weil wir können. Betrachten wir nun die Wellenfunktion $ - \ psi $, die $ N \ psi $ mit $ N = -1 $ entspricht. Ist diese neue Wellenfunktion normalisiert?

$$ \ begin {align} \ int _ {- \ infty} ^ {\ infty} \! \ lvert - \ psi \ rvert ^ 2 \, \ mathrm {d} x & = \ lvert -1 \ rvert ^ 2 \! \! \ int _ {- \ infty} ^ {\ infty} \! \ lvert \ psi \ rvert ^ 2 \, \ mathrm {d} x \\ & = \ int _ {- \ infty} ^ {\ infty} \! \ lvert \ psi \ rvert ^ 2 \, \ mathrm {d} x \\ & = 1 \ end {align} $$

Natürlich ist es das. Was ich bisher geschrieben habe, lautet also im Grunde: Wenn $ \ psi $ eine normalisierte Lösung für die Schrödinger-Gleichung ist, ist dies auch $ - \ psi $ .

Tatsächlich Sie könnten noch einen Schritt weiter gehen. Mit genau der gleichen Arbeitsweise wie oben könnten Sie zeigen, dass, wenn $ \ psi $ eine normalisierte Lösung der Schrödinger-Gleichung ist, die Wellenfunktion $ (a + ib) \ psi $ auch eine wäre, solange $ a ^ 2 + b ^ 2 = 1 $. (Wenn Sie Exponentiale mögen, entspricht dies $ a + ib = e ^ {i \ theta} $.) Ich habe diese Idee in diesem Diagramm veranschaulicht:

$ \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad $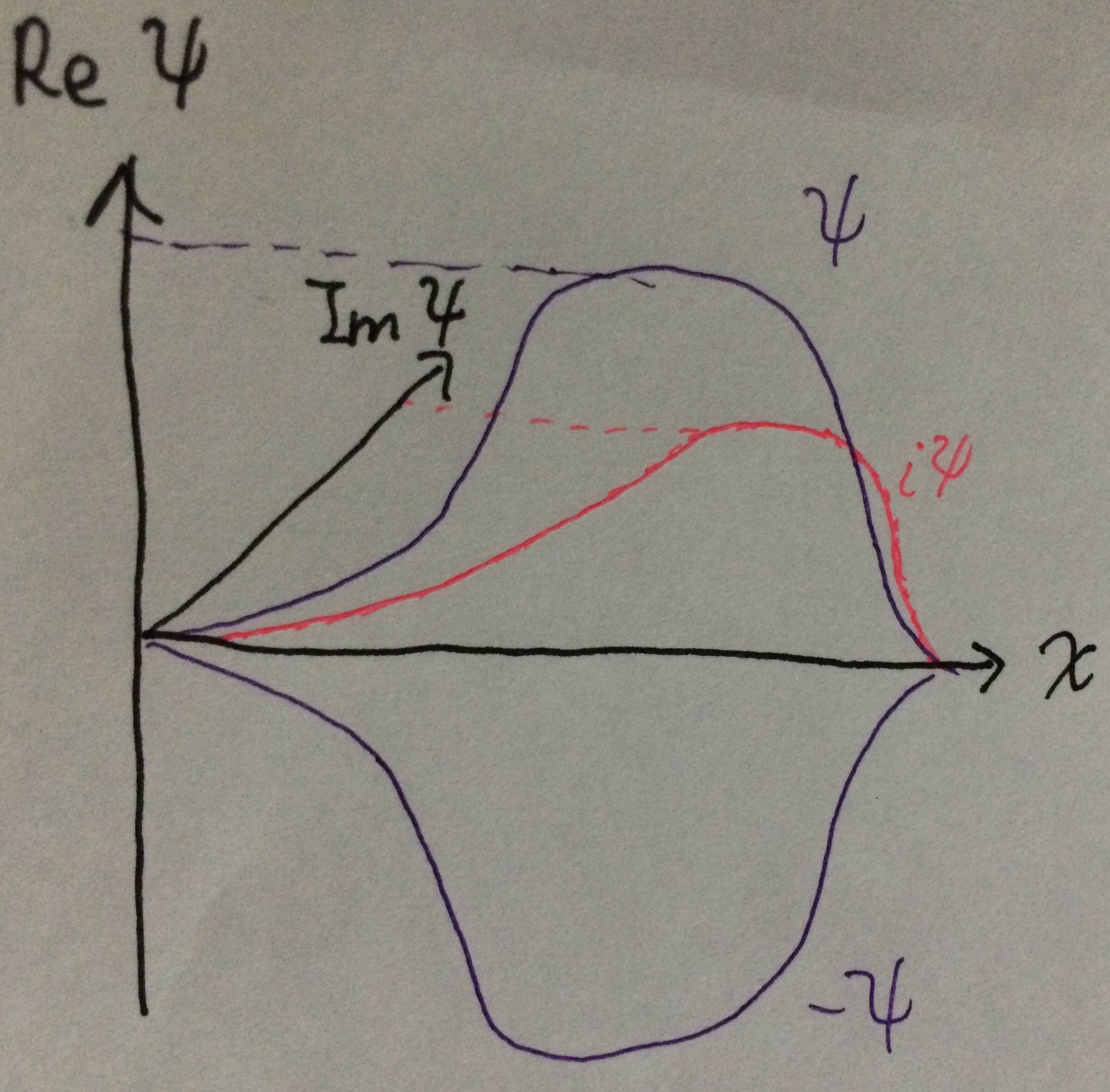

Wenn $ \ psi $ eine eindimensionale Wellenfunktion mit realem Wert ist, können Sie sie in einem Diagramm gegen $ x $ darstellen. Die Wellenfunktion $ i \ psi $ hätte dann genau die gleiche Form und würde nur aus der Papierebene herauskommen ($ \ theta = 90 ^ \ circ $). Sie könnten die Wellenfunktion $ (1 + i) \ psi / \ sqrt {2} $ haben. Es würde um $ \ theta = 45 ^ \ circ $ nach außen aus der Papierebene zeigen, genau auf halber Strecke zwischen $ \ psi $ und $ i \ psi $, aber genau in der gleichen Form. Die Physik weiß jedoch nicht, wo sich die Ebene Ihres Papiers befindet, daher sind alle diese Wellenfunktionen gleichermaßen zulässig. Aus Sicht des Systems sind sie alle dasselbe.

Verwenden der Wellenfunktion

"Aber warten Sie! Wenn die Wellenfunktion negativ ist, was? über die Werte von Impuls, Position und Energie, die Sie berechnen? Werden sie negativ? "

" Gute Frage, ich selbst! "

Nun, für den Anfang ist eine Sache, für die Sie die Wellenfunktion verwenden, die Wahrscheinlichkeitsdichte $ P (x) $ zu finden. Nach Max Borns Interpretation der Wellenfunktion ist dies gegeben durch $ P (x) = \ lvert \ psi \ rvert ^ 2 $. Angenommen, die durch die negative Wellenfunktion $ - \ psi $ beschriebene Wahrscheinlichkeitsdichte ist eine andere Funktion von $ x $, die als $ Q (x) $ bezeichnet wird:

$$ \ begin {align} Q (x ) = \ lvert - \ psi \ rvert ^ 2 & = \ lvert -1 \ rvert ^ 2 \ lvert \ psi \ rvert ^ 2 \\ & = \ lvert \ psi \ rvert ^ 2 \\ & = P (x) \ end {align} $$

Die durch die negative Wellenfunktion beschriebene Wahrscheinlichkeitsdichte ist also genau gleich. Tatsächlich ist die durch $ i \ psi $ beschriebene Wahrscheinlichkeitsdichte ebenfalls genau dieselbe.

Lassen Sie uns nun über Observable sprechen, wie z. B. Position $ x $, Momentum $ p $ und Energie $ E $. Jedes Observable hat einen entsprechenden Operator: $ \ hat {x} $, $ \ hat {p} $ und $ \ hat {H} $ (der Hamiltonianer hat einen speziellen Buchstaben, weil er nach William Hamilton benannt ist) a>). Mit diesen Operatoren berechnen Sie den Mittelwert des Observablen. Ich werde ein Beispiel bezüglich der Dynamik geben. Wenn Sie den mittleren Impuls mit der Bezeichnung $ \ langle p \ rangle $ ermitteln möchten, gehen Sie wie folgt vor:

$$ \ begin {align} \ langle p \ rangle & = \ langle \ psi \ lvert \ hat {p} \ rvert \ psi \ rangle \\ & = \ int _ {- \ infty} ^ \ infty \! \ psi ^ * \ hat {p} \ psi \, \ mathrm {d} x \ end { align} $$

Ich werde den Wert dieses Integrals $ p_1 $ aufrufen. Lassen Sie uns jetzt das Gleiche tun. Nehmen wir an, dass der mittlere Impuls für die negative Wellenfunktion nicht unbedingt der gleiche Wert ist. Nennen wir den neuen mittleren Impuls etwas anderes, wie $ p_2 $.

Bevor wir fortfahren, werde ich feststellen, dass der Impulsoperator $ \ hat {p} = -i \ hbar \ frac {\ mathrm {d}} {\ mathrm {d} x} $ ebenfalls linear ist . Wenn Sie daran zweifeln, können Sie es anhand der Definition der Linearität im allerersten Link testen, den ich gepostet habe. Tatsächlich sind alle quantenmechanischen Operatoren, die Observablen entsprechen, linear. Daher $ \ hat {p} (- \ psi) = - \ hat {p} \ psi $ und so:

$$ \ begin {align} p_2 & = \ langle - \ psi \ lvert \ hat {p} \ lvert- \ psi \ rangle \\ & = \ int _ {- \ infty} ^ \ infty \! (- \ psi) ^ * \ hat {p} (- \ psi) \, \ mathrm {d} x \\ & = (-1) ^ 2 \! \! \ int _ {- \ infty} ^ \ infty \ ! \ psi ^ * \ hat {p} \ psi \, \ mathrm {d} x \\ & = \ int _ {- \ infty} ^ \ infty \! \ psi ^ * \ hat {p} \ psi \, \ mathrm {d} x \\ & = p_1 \ end {align} $$

Wenn wir also über den Grundzustand des Partikels sprechen in einer Box mit der Länge $ L $, unabhängig davon, ob Sie die positive Wellenfunktion verwenden

$$ \ psi_1 = \ sqrt {\ frac {2} {L}} \ sin {\ left (\ frac { \ pi x} {L} \ right)} $$

oder die negative Wellenfunktion

$$ - \ psi_1 = - \ sqrt {\ frac {2} {L}} \ sin {\ left (\ frac {\ pi x} {L} \ right)} $$

oder die komplexe Wellenfunktion

$$ i \ psi_1 = i \ sqrt { \ frac {2} {L}} \ sin {\ left (\ frac {\ pi x} {L} \ right)} $$

Sie erhalten genau die gleichen Werte für die durchschnittliche Position $ (= L / 2) $, durchschnittlicher Impuls $ (= 0) $ und durchschnittliche Energie $ (= h ^ 2 / 2mL ^ 2) $ (das Wort Durchschnitt ist hier redundant, da dies ein stationärer Zustand ist, aber was auch immer)

Alles, was ich bisher gesagt habe, kann leicht auf drei Dimensionen verallgemeinert werden. Es kann auch auf lineare Kombinationen stationärer Zustände verallgemeinert werden, dh Lösungen der zeitabhängigen Schrödinger-Gleichung.

Eine Anmerkung zu Molekülorbitalen

"Okay, aber was passiert, wenn Sie Atomorbitale zu Molekülorbitalen kombinieren? Sie haben konstruktive Interferenzen durch die positive + positive und destruktive Interferenz durch die positive + negative, aber was ist mit der negativen + negativen Kombination?"

"Gute Frage, ich selbst!"

Lassen Sie uns über das $ \ ce {H2} $ -Molekül sprechen. Der richtige Weg, um die Molekülorbitale zu finden, besteht darin, die Schrödinger-Gleichung für das gesamte System zu lösen, was wirklich schwierig ist. Eine Möglichkeit, ungefähre Formen der MOs zu finden, besteht darin, lineare Kombinationen von Atomorbitalen zu erstellen. Diese Methode wird als LCAO-Näherung bezeichnet. Nennen wir das 1s-Orbital des Wasserstoffs links $ \ phi_1 $ und das 1s-Orbital des Wasserstoffs rechts $ \ phi_2 $. In den vorhergehenden Abschnitten haben wir bereits festgestellt, dass für das Wasserstoffatom die einzelnen Phasen von $ \ phi_1 $ und $ \ phi_2 $ keine Rolle spielen . Nehmen wir der Einfachheit halber an, dass ihre Phasen beide positiv sind.

Nach dem, was Sie bereits wissen, können Sie zwei Molekülorbitale $ \ psi_1 $ und $ \ psi_2 $ erhalten:

$$ \ begin {align} \ psi_1 & = \ phi_1 + \ phi_2 \\\ psi_2 & = \ phi_1 - \ phi_2 \ end {align} $$

Dies sind die bindenden und antibindenden Orbitale jeweils (zumindest innerhalb einer Normalisierungskonstante, die mir hier nicht wichtig ist, da die Details irrelevant sind). Lassen Sie uns nun über die Kombinationen sprechen, die wir verpasst haben.

$$ \ begin {align} - \ phi_1 - \ phi_2 & = - \ psi_1 \\ - \ phi_1 + \ phi_2 & = - \ psi_2 \ end {align} $$

Wir haben bereits gesagt, dass $ \ psi_1 $ und $ \ psi_2 $ (Annäherungen an) Lösungen für die Schrödinger-Gleichung sind. Das bedeutet, dass nach dem, worüber wir zuvor gesprochen haben, $ - \ psi_1 $ und $ - \ psi_2 $ auch (Annäherungen an) Lösungen für die Schrödinger-Gleichung sein müssen. Sie müssen die gleichen Energien wie $ \ psi_1 $ und $ \ psi_2 $ haben. Soweit das Molekül weiß (und sich darum kümmert), sind sie dasselbe wie $ \ psi_1 $ und $ \ psi_2 $.

Nun, seitdem Die einzelnen Phasen der Atomorbitale spielen keine Rolle. Wenn Sie wirklich möchten, können Sie der ganzen Welt erklären, dass Sie Folgendes definieren:

$$ \ phi_3 = \ phi_1 \ text {und} \ phi_4 = - \ phi_2 $$

$$ \ begin {align} \ psi_1 & = \ phi_3 - \ phi_4 \\\ psi_2 & = \ phi_3 + \ phi_4 \ end {align} $$

Die Koeffizienten der Atomorbitale müssten unterschiedlich sein, da Sie darauf bestanden , sie in verschiedenen Phasen zu haben - jedoch Das Ergebnis ist das gleiche! Sie erhalten ein bindendes MO und ein antibindendes MO.

Meine Verwirrung rührt daher, dass ich keine Ahnung habe, was eine negative Wellenfunktion darstellt. Kann mir jemand eine physikalische Vorstellung davon geben, wie diese negative Wellenfunktion mit etwas in der Realität korreliert werden könnte?

Ihre Verwirrung beruht größtenteils auf zwei Dingen:

1. Sie verwenden die falschen Begriffe wie "positive" oder "negative" Wellenfunktion, die dies zeigen Sie verstehen nicht ganz, was hier mathematisch vor sich geht. Dies ist besonders wichtig, wenn man den zweiten Punkt berücksichtigt.

2. Sie suchen nach einer physischen Intuition hinter einem rein mathematischen Modell, das sehr wenig mit der physischen Realität zu tun hat. P. >

ol>

---

Definieren wir aus Gründen der Argumentation eine positive Funktion einer einzelnen reellen Variablen $ x $ als eine reelle Funktion, die nur positive Werte annimmt, dh $ f (x) > 0 $ für alle $ x $ und eine negative Funktion als Funktion, die nur negative Werte annimmt, dh so dass $ f (x) < 0 $ für alle $ x $. Ich denke, das ist etwas, was OP im Kopf hat, wenn es um "positive" und "negative" Wellenfunktionen geht. Aber die Art und Weise, wie OP diese Adjektive verwendet, um zu beschreiben, womit er Probleme hat, ist sicherlich falsch, da bei einer Wellenfunktion $ \ psi (x) $, woher weißt du, dass es eine positive oder eine negative ist? Offensichtlich wissen Sie das nicht und können folglich auch nicht sagen, ob $ - \ psi (x) $ positiv oder negativ ist.

Diese ganze LCAO-MO Das Geschäft hat einfach nichts damit zu tun, dass Wellenfunktionen positiv oder negativ sind, sondern es geht darum, zwei orthogonale lineare Kombinationen zweier Atomorbitale (AO) zu bilden, um zwei im Wesentlichen unterschiedliche Molekülorbitale (MO) zu bilden. Nanoputian hat diesen einfachen LCAO-MO-Formalismus für den speziellen Fall des $ \ ce {H2} $ -Moleküls in seiner Antwort ausführlich beschrieben, und hier möchte ich OP (und andere) nur vor der Gefahr von warnen Nehmen Sie dieses Bild wörtlich.

MOs werden aus AOs in einem mathematischen und nicht physischen Sinne gebildet. Es ist nur ein Spiel mit Zahlen: Nehmen Sie AOs und schreiben Sie MOs als lineare Kombinationen davon. Man sollte nicht denken, dass dieses primitive LCAO-MO-Modell mit bindenden und anti-bindenden MOs, die als Ergebnis einer konstruktiven und destruktiven Interferenz der entsprechenden AOs gebildet wurden, reale physikalische Prozesse beschreibt. Wie gesagt, dieses Modell hat sehr wenig mit der Realität zu tun.

Zusätzlich zu anderen Antworten und sehr kurz wird eine Bindung gebildet, wenn zwischen den Kernen eine große Elektronendichte besteht, wodurch die gesamte potentielle Energie verringert wird. Umgekehrt ist die potentielle Energie höher, wenn zwischen den Atomen nicht viel Elektronendichte vorhanden ist, und dies ist eine Anti-Bindung. Wir identifizieren Anti-Bonding, indem wir nach Knoten zwischen Atomen suchen. Als Faustregel gilt: Je mehr Knoten vorhanden sind, desto höher ist die Energie und damit die Anti-Bindung.

Beim Addieren oder Subtrahieren oder Multiplizieren von Wellenfunktionen gelten die normalen Regeln der Mathematik, da Wellenfunktionen durch normale mathematische Gleichungen dargestellt werden. Wir müssen uns daran erinnern, dass sie oft in Polarkoordinaten anstelle der üblichen x, y, z dargestellt werden und daher möglicherweise nicht so vertraut erscheinen, z. Formen von s-, p-, d-Orbitalen.

Das Vorzeichen einer Wellenfunktion $ \ psi $ ist nur ein Teil ihrer mathematischen Beschreibung. Einige Wellenfunktionen haben positive und negative Teile, z. räumlicher Teil von p-Orbitalen, einige werden durch komplexe Zahlen dargestellt, z. einige d Orbitale. Wir können $ - \ psi $ gleich $ \ psi $ sein lassen, da die Wahrscheinlichkeit, das Teilchen in einem kleinen Bereich des Raums $ \ tau $ bis $ \ tau + d \ tau $ zu finden, $ \ psi ^ 2d \ tau ist $.
Der gemessene Wert einer Eigenschaft, X, z. Position, wird durch den Erwartungs- (oder Durchschnitts-) Wert gegeben; $ <X> = \ int \ psi ^ * X \ psi d \ tau $, also spielt das Vorzeichen von $ \ psi $ keine Rolle. ($ \ psi ^ * $ ist das komplexe Konjugat, was nur wichtig ist, wenn $ \ psi $ eine komplexe Zahl ist.) Beim Hinzufügen von Wellenfunktionen, um eine lineare Kombination zu bilden, z. $ \ psi = s_1-s_2 + s_3 $ ist dasselbe wie $ - \ psi = -s_1 + s_2-s_3 $.

Chemiker verwenden häufig Diagramme mit dem Vorzeichen der Wellenfunktion, die als $ \ pm $ gekennzeichnet oder auf eine bestimmte Weise gefärbt sind, um das Verständnis der Bindung zu erleichtern. Es ist eine sehr nützliche Abkürzung im Vergleich zur Berechnung von Dingen. Die folgende Abbildung zeigt einige Beispiele.

Die p-Orbitale addieren 'in Phase' als $ p_z + p_z $ (Bindung) und außer Phase als $ p_z-p_z $ (Anti-Bindung). Die Schattierung auf den Orbitalen zeigt das "Vorzeichen" der Wellenfunktion. In $ p_z-p_z $ ist die Differenz nicht überall Null, da die Orbitale unterschiedliche Ursprünge haben, da sie entlang der Bindungsachse verschoben sind. Die Differenz ist jedoch im Mittelpunkt Null, und dies wird als Knoten bezeichnet.
Die Regeln lauten, dass dieselbe Schattierung addiert und unterschiedliche Schattierungen subtrahiert.
Das $ s + p_z $ ist nicht bindend, da sich das s-Orbital mit beiden Teilen des p-Orbitals überlappt und sich die beiden Überlappungen aufheben.
Die drei s-Orbitale können addieren, alle drei gleichen Farbtöne bilden eine Bindung (grau oder weiß ist gleich, $ s_1 + s_2 + s_3 $ entspricht $ -s_1-s_2-s_3 $) oder subtrahieren Orbitale, sagen wir als $ s_1-s_2 + s_3 $ ist Anti-Bonding.

Sie haben dieses Missverständnis, weil Sie vergessen, dass eine Wellenfunktion eine Welle ist !!!. Wellen können entweder in Phase oder außer Phase sein. All diese Begriffe negativer und positiver Wellen haben Ihren Geist dazu gebracht, nicht verwandte Konzepte zu mischen.

Stellen Sie sich ein isoliertes H-Atom vor, Sie können sich fragen, wie die Phase seiner Wellenfunktion ist, und die Antwort lautet: Wer kümmert sich oder über welche Phase sprichst du?. Die Phase hat nur dann eine physikalische Bedeutung, wenn sie wie die Überlagerung von Wellen beobachtet werden kann. Dann ist es sinnlos, nach der Bedeutung einer "negativen" Wellenfunktion zu fragen.

Denken Sie an die Überlagerung von EM-Wellen oder String-Wellen. Sie fragen nicht nach der Bedeutung einer "negativen" Saitenwelle, Sie sprechen von einer phasenverschobenen Saitenwelle in Bezug auf eine andere. Das Obige ist genau das gleiche, jedoch mit quantenmechanischen Wellen.

Die Verwendung von "+" und "-" Zeichen ist ein praktisches mathematisches Werkzeug, um die Phasendifferenz zu beschreiben, aber Sie können auch eine andere Sache wie Farben verwenden.

Ich erwarte, dass die oben genannten Durch Klarstellung können Sie wirklich verstehen, wie die LCAO-MO-Theorie funktioniert.